QR factorization
For any matrix A (m x n), m >= n we can calculate its QR factorization A= Q*R, where Q (m x m) is an orthogonal matrix and R (m x n) is defined as
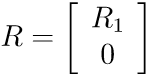
where R1 (n x n) is an upper triangular matrix. For more details see this Wikipedia article.
Solving least squares problems
Assume an overdetermined linear system A*x = b with A (m x n), m >= n and rank(A) = n. This linear system does not have a solution, but we can find a vector x that minimizes ||b-A*x||, which is equal to the sum of squares of entries of b - A*x. This is called a least squares problem. The solution of the least squares problem is
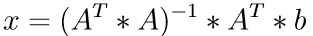
By applying the QR factorization, the above equation leads to
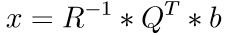
where the multiplication with R-1 is implemented as a forward substitution with the upper triangular matrix R1. For more details see this video.
LQ factorization
For any matrix A (m x n), m <= n we can calculate its LQ factorization A= L*Q, where Q (n x n) is an orthogonal matrix and L (m x n) is defined as
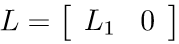
where L1 (m x m) is a lower triangular matrix. For more details see this.
Solving minimum norm problems
Assume an underdetermined linear system A*x = b with A (m x n), m < n and rank(A) = m. This linear system has an infinite number of solutions. In this case it is often useful to find the unique solution that minimizes ||x||2. This is called a minimum norm problem. The solution of the min norm problem is
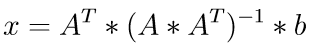
By applying the LQ factorization, the above equation leads to
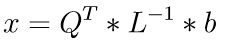
where the multiplication with L-1 is implemented as a back substitution with the lower triangular matrix L1. For more details see this.