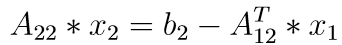Schur complement

Let us seprarate the rows and columns of a symmetric matrix A into 2 groups and define the block submatrices:

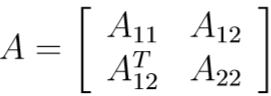
If A₂₂ is invertible, the Schur complement of the block A₂₂ is defined as:

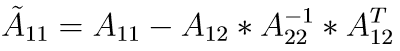
The Schur complement is important in many applications, such as domain decomposition methods, homogenization, etc, and has some interesting properties: e.g. if A is symmetric positive definite, then so is the Schur complement of A₂₂ and vice-versa. For more details see this wikipedia article.

Static condensation

Let us apply the previous decomposition to a linear system A*x = b:

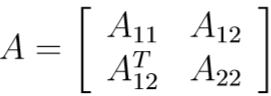
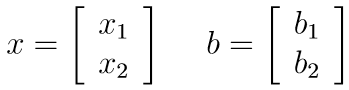
Suppose we need to work only with the group 1 of rows/columns, without completely disregarding the contribution of group 2. In this case we typically condense the submatrix A₂₂ using its Schur complement. We also condense the subvector b₂:

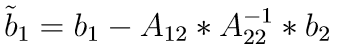
Then we can solve the system with respect to x₁ only:

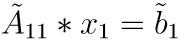
If x₂ is needed, it can be calculated afterwards by solving the linear system: